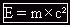
En 1905, Albert Einstein postule que la masse est une des formes que peut prendre l'énergie. Un système au repos, de masse m, possède une énergie de masse E donnée par la relation d'Einstein :
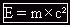 |
E (en J) |
| m (en Kg) | |
| c = 3,0.108 m/s |
Cette relation est appelée relation d'équivalence entre la masse et l'énergie. Elle entraîne que toute variation de masse Dm d'un système au repos correspond à une variation de son énergie de masse DE telle que:
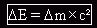
Si la masse d'un système au repos diminue aussi (DE < 0), l'énergie DE est libérée par le système et fournie au milieu extérieur.
C'est le cas du Soleil
Il y a fusion nucléaire lorsque deux noyaux légers s'unissent au cours d'un choc pour former un noyau plus lourd.
Exemple:
Lors du choc, un noyau d'hélium plus lourd et un neutron sont formés. Le bilan de la fusion respecte les lois de conservation de Soddy (conservation du nombre de masse et du nombre de charge) et s'écrit :

Les deux noyaux chargés positivement doivent posséder une très grande énergie pour vaincre les forces de répulsions électriques et se rapprocher suffisamment pour que la fusion se produise. Il faut, pour cela, que le milieu soit porté à très haute température, de l'ordre de 108 K. Ainsi, la réaction de fusion nucléaire est appelée réaction thermonucléaire. A ces très hautes températures, la matière est à l'état de plasma (le 4e état de la matière).
Dans le Soleil, la fusion des noyaux d'hydrogène, à température voisine de 1,5.107 K, donne des noyaux d'hélium après plusieurs réaction de fusion:
| Réactions se produisant dans le Soleil | Enégie produite |
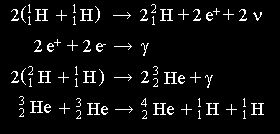 |

|
 |
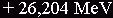 |
Avec Qpp l'énergie disponible pour l'étoile.
L'énergie perdue sous forme de neutrinos (n) est égale à 0, 526 MeV, soit 2 % du totale produit : 1 MeV = 1,6.10-13 J.
n : particule sans masse se déplaçant à la célérité de la lumière, et appelée des neutrinos
Cette chaîne de réaction est appelée chaîne p-p, c'est la chaîne de réactions qui prédomine dans le Soleil.
On a vu que la masse est une forme de l'énergie ; si le noyau est en mouvement, il possède de l'énergie cinétique Ec. On admettra que son énergie totale est la somme E + Ec de ces deux énergie. Considérons un système isolé formé par des noyaux participant à la réaction nucléaire:
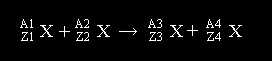
Le système est isolé, donc, son énergie totale se conserve :
(E1 + Ec1) + (E1 + Ec2) = (E3 + Ec3) + (E4 + Ec4)
Une réaction qui se fait avec une perte de masse (DE < 0) libère de l'énergie sous forme cinétique (DEc > 0).
Toute réaction nucléaire s'effectuant avec perte de masse fournit de l'énergie au milieu extérieur.
Depuis qu'il rayonne, le Soleil a perdu 6,24.10 26 Kg au rythme de 4,3.10 9 Kg/s. On peut calculer cette perte de masse d' après la relation d'Einstein, Dm = P/c².
Le Soleil a donc libéré une énergie E telle que E = Dmc² soit 5,61.10 43 J.